容斥原理是概率统计中的一条定理,它主要用来求一些集合的并集,由于这些集合可能有交集,所以它们的并集可能不是简单的相加减,而容斥原理,就可以很好地用数学公式的形式来求得集合的并集
容斥原理
原理:
先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
公式:
$(A_{1} \cup A_{2} \cup A_{3} \cup ... \cup A_{n})=\sum_{0<i\le n} A_{i}-\sum_{0<i<j\le n} (A_{i} \cap A_{j})+\sum_{0<i<j<k\le n}(A_{i}\cap A_{j}\cap A_{j})+...+(-1)^{n+1}(A_{1} \cap A_{2}\cap A_{3}\cap ... \cap A_{n}) $
ps:这公式我也记不住,放在这里只是摆设,下面我将介绍容斥原理的基本逻辑
容斥原理,容的是单一,斥的是重复,如下图ven图所示:
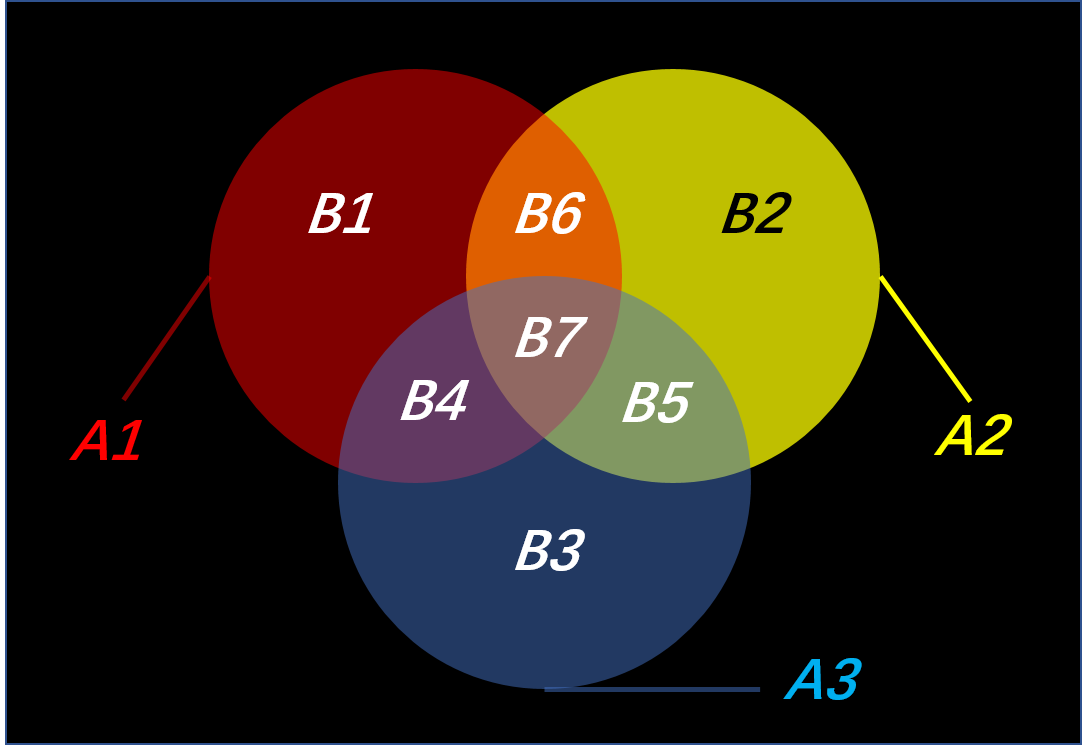
从图中可以看到:
$A_{1},A_{2},A_{3}$为三个事件,它们各有属于自己独立的事件,也有和其他事件相交的事件,正因为如此,如果要求三个事件的并集,并不只是简单的把三个事件通过直接加和来得到,还需将重复的部分给“斥”出去。
如图所示:$A_{1}=B_{1} \cup B_{4} \cup B_{6} \cup B_{7}$
$A_{2}=B_{2} \cup B_{5} \cup B_{6} \cup B_{7}$
$A_{3}=B_{3} \cup B_{4} \cup B_{5} \cup B_{7}$
故:$A_{1} \cup A_{2} \cup A_{3}=B_{1} \cup B_{2} \cup B_{3} \cup B_{4} \cup B_{5} \cup B_{6} \cup B_{7}$
接下来,需要把$A_{1} \cup A_{2} \cup A_{3}$变形:
(1) 先求$A_{1}+ A_{2}+ A_{3}$(全“容”)
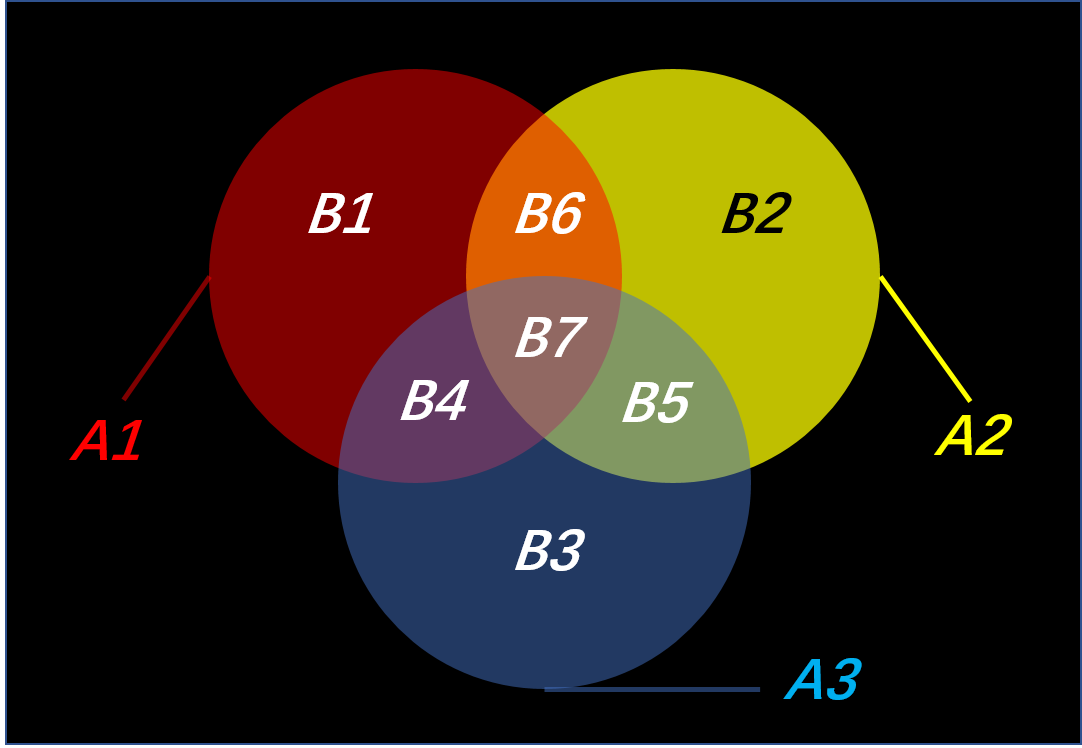
(2) 已知$A_{1}+ A_{2}+ A_{3}$包括了$A_{1} \cup A_{2} \cup A_{3}$,但$A_{1},A_{2},A_{3}$两两相交的部分($B_{6}+B_{7},B_{4}+B_{7},B_{5}+B_{7}$)被包含了两次,于是需要将这些重复的部分“斥”掉(选“斥”),得到:
$A_{1}+ A_{2}+ A_{3}- (B_{6}+ B_{7}+ B_{4}+ B_{7}+ B_{5}+ B_{7})=A_{1}+ A_{2}+ A_{3}$
$-(A_{1} \cap A_{2}+ A_{1} \cap A_{3}+ A_{2} \cap A_{3})$
(3) 虽然减掉了重复的部分,但是发现$A_{1},A_{2},A_{3}$所具有的的共同事件$B_{7}$被重复“斥”掉了一次,需要将$B_{7}$“容回来”(选“容”),得到$A_{1} \cup A_{2} \cup A_{3}$:
$A_{1}+ A_{2}+ A_{3}- (B_{6}+ B_{7}+ B_{4}+ B_{7}+ B_{5}+ B_{7})+B_{7}=A_{1}+ A_{2}+ A_{3}$
$-(A_{1} \cap A_{2}+ A_{1} \cap A_{3}+ A_{2} \cap A_{3})+ A_{1} \cap A_{2}\cap A_{3}$
最后:
$A_{1}+ A_{2}+ A_{3}=\sum_{0<i\le 3} A_{i}$
$A_{1} \cap A_{2}+ A_{1} \cap A_{3}+ A_{2} \cap A_{3}=\sum_{0<i<j\le 3} (A_{i} \cap A_{j})$
$A_{1} \cap A_{2}\cap A_{3}=\sum_{0<i<j<k\le n}(A_{i}\cap A_{j}\cap A_{j})$
得到:
$A_{1} \cup A_{2} \cup A_{3}=\sum_{0<i\le 3} A_{i}-\sum_{0<i<j\le 3} (A_{i} \cap A_{j})+\sum_{0<i<j<k\le n}(A_{i}\cap A_{j}\cap A_{j})$(n=3的容斥原理)
从这个例子,我们可以看出,容斥原理的公式就是容(+)与斥(-)不断平衡的过程,在平衡中不断靠近最终结果,直到最后一次平衡:“容”(“斥”)了所有事件的交集之后,就可以得到所有事件的并集。
将n=3的容斥原理推广得到容斥原理:
$(A_{1} \cup A_{2} \cup A_{3} \cup ... \cup A_{n})=$
$\sum_{0<i\le n} A_{i}$
$-\sum_{0<i<j\le n} (A_{i} \cap A_{j})$
$+\sum_{0<i<j<k\le n}(A_{i}\cap A_{j}\cap A_{j})$
$-\sum_{0<i<j<k<l\le n}(A_{i}\cap A_{j}\cap A_{j}\cap A_{j})$
$+...$
$+(-1)^{n+1}(A_{1} \cap A_{2}\cap A_{3}\cap ... \cap A_{n}) $
例题
1.牛客练习赛44----C-小y的质数: